Calculus AB compatible with AP*
This is the ultimate AP Calculus AB study aid! Award-winning professor Edward Burger teaches the fundamentals of Calculus AB in dynamic video lessons. You'll learn the calculus concepts you need to score a perfect 5 on the AP Calculus AB exam. And it's available whenever you need it for one flat price, so it's better than a tutor.
This is not a test preparation product in the sense of providing exam-taking tips; it's a full course geared to AP-caliber work. You can use it alongside your AP classroom at school, reinforcing what you've learned so that you'll make the score you need on the AP Calculus AB exam. It's filled with calculus tutorials that provide AP Calculus instruction that fits your schedule. We explain calculus limits step by step, so that they're easy to remember when it's time for your AP Calculus AB exam. Thinkwell's online Calculus AB subscription is a complete web-based solution that includes all the content you'll need to succeed in AP Calculus AB.
Our complete Calculus AB compatible with AP* package includes:- 12-month Online Subscription to our complete Calculus AB course with video lessons, automatically graded calculus problems, and much more
- Printed Notes (optional, AB + BC) are the AP Calculus course notes from the Online Subscription printed in a black & white, on-the-go format. These are available for purchase from the AP Calculus AB Course Site.
Printed Notes require the purchase of an online subscription.
(*AP is a registered trademark of the College Board, which was not involved in the production of, and does not endorse, this product.)
Risk-Free Three-DayMoney-Back Guarantee
Calculus AB compatible with AP* Materials
Online Subscription, 12-month access
Access to a complete online package that includes everything you need.
- Thinkwell's video lectures cover the comprehensive scope and sequence of topics covered on the AP Calculus AB exam.
- Our automatically graded exercises with immediate feedback allow you to quickly determine which areas you'll need to spend extra time studying.
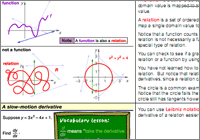
- Concise, illustrated review notes help you distill the fundamental ideas, concepts, and formulas from Calculus you'll need to know in order to succeed on the AP Calculus exam.
- Subscriptions start when you are ready. Buy now and activate your course anytime you like. Wait up to one year to activate your subscription; your 12-month subscription doesn't begin until you say so!
Calculus AB compatible with AP* Details
Thinkwell's Calculus AB includes all of these features to prepare you for the big exam:
- Equivalent to 11th- or 12th-grade AP Calculus AB
- More than 180 video lessons (see sample)
- 1000+ interactive AP Calculus AB problems with immediate feedback allow you to track your progress (see sample)
- Calculus AB practice chapter tests for all 12 chapters, as well as a final exam to make sure you're ready for the AP Calculus AB exam (only available in the homeschool version).
- Printable illustrated notes for each topic
- Real-world application examples in both lectures and exercises
- Closed captioning for all videos
- Glossary of more than 200 mathematical terms
- Engaging content to help students advance their mathematical knowledge:
- Understanding and evaluating limits and derivatives
- Computational techniques such as the power rule, product rule, quotient rule, and chain rule
- Trigonometric, exponential, and logarithmic functions
- Implicit differentiation
- Differentiation, optimization, and related rates
- Sketching curves
- Antiderivatives, integration, and the fundamental theorem of calculus
- Applications of integration such as motion, finding the area between two curves, and integrating with respect to y
Table of Contents
(Expand All - Close All)1. The Basics
- 1.1 Overview
- 1.1.1 An Introduction to Thinkwell Calculus
- 1.1.2 The Two Questions of Calculus
- 1.1.3 Average Rates of Change
- 1.1.4 How to Do Math
- 1.2 Precalculus Review
- 1.2.1 Functions
- 1.2.2 Graphing Lines
- 1.2.3 Parabolas
- 1.2.4 Some Non-Euclidean Geometry
2. Limits
- 2.1 The Concept of the Limit
- 2.1.1 Finding Rate of Change over an Interval
- 2.1.2 Finding Limits Graphically
- 2.1.3 The Formal Definition of a Limit
- 2.1.4 The Limit Laws, Part I
- 2.1.5 The Limit Laws, Part II
- 2.1.6 One-Sided Limits
- 2.1.7 The Squeeze Theorem
- 2.1.8 Continuity and Discontinuity
- 2.2 Evaluating Limits
- 2.2.1 Evaluating Limits
- 2.2.2 Limits and Indeterminate Forms
- 2.2.3 Two Techniques for Evaluating Limits
- 2.2.4 An Overview of Limits
3. An Introduction to Derivatives
- 3.1 Understanding the Derivative
- 3.1.1 Rates of Change, Secants, and Tangents
- 3.1.2 Finding Instantaneous Velocity
- 3.1.3 The Derivative
- 3.1.4 Differentiability
- 3.2 Using the Derivative
- 3.2.1 The Slope of a Tangent Line
- 3.2.2 Instantaneous Rate
- 3.2.3 The Equation of a Tangent Line
- 3.2.4 More on Instantaneous Rate
- 3.3 Some Special Derivatives
- 3.3.1 The Derivative of the Reciprocal Function
- 3.3.2 The Derivative of the Square Root Function
4. Computational Techniques
- 4.1 The Power Rule
- 4.1.1 A Shortcut for Finding Derivatives
- 4.1.2 A Quick Proof of the Power Rule
- 4.1.3 Uses of the Power Rule
- 4.2 The Product and Quotient Rules
- 4.2.1 The Product Rule
- 4.2.2 The Quotient Rule
- 4.3 The Chain Rule
- 4.3.1 An Introduction to the Chain Rule
- 4.3.2 Using the Chain Rule
- 4.3.3 Combining Computational Techniques
5. Special Functions
- 5.1 Trigonometric Functions
- 5.1.1 A Review of Trigonometry
- 5.1.2 Graphing Trigonometric Functions
- 5.1.3 The Derivatives of Trigonometric Functions
- 5.1.4 The Number Pi
- 5.2 Exponential Functions
- 5.2.1 Graphing Exponential Functions
- 5.2.2 Derivatives of Exponential Functions
- 5.3 Logarithmic Functions
- 5.3.1 Evaluating Logarithmic Functions
- 5.3.2 The Derivative of the Natural Log Function
- 5.3.3 Using the Derivative Rules with Transcendental Functions
6. Implicit Differentiation and the Inverse Function
- 6.1 Implicit Differentiation Basics
- 6.1.1 An Introduction to Implicit Differentiation
- 6.1.2 Finding the Derivative Implicitly
- 6.2 Applying Implicit Differentiation
- 6.2.1 Using Implicit Differentiation
- 6.2.2 Applying Implicit Differentiation
- 6.3 Inverse Functions
- 6.3.1 The Exponential and Natural Log Functions
- 6.3.2 Differentiating Logarithmic Functions
- 6.3.3 Logarithmic Differentiation
- 6.3.4 The Basics of Inverse Functions
- 6.3.5 Finding the Inverse of a Function
- 6.4 The Calculus of Inverse Functions
- 6.4.1 Derivatives of Inverse Functions
- 6.5 Inverse Trigonometric Functions
- 6.5.1 The Inverse Sine, Cosine, and Tangent Functions
- 6.5.2 The Inverse Secant, Cosecant, and Cotangent Functions
- 6.5.3 Evaluating Inverse Trigonometric Functions
- 6.6 The Calculus of Inverse Trigonometric Functions
- 6.6.1 Derivatives of Inverse Trigonometric Functions
- 6.7 The Hyperbolic Functions
- 6.7.1 Defining the Hyperbolic Functions
- 6.7.2 Hyperbolic Identities
- 6.7.3 Derivatives of Hyperbolic Functions
7. Applications of Differentiation
- 7.1 Position and Velocity
- 7.1.1 Acceleration and the Derivative
- 7.1.2 Solving Word Problems Involving Distance and Velocity
- 7.2 Linear Approximation
- 7.2.1 Higher-Order Derivatives and Linear Approximation
- 7.2.2 Using the Tangent Line Approximation Formula
- 7.2.3 Newton's Method
- 7.3 Optimization
- 7.3.1 The Connection Between Slope and Optimization
- 7.3.2 The Fence Problem
- 7.3.3 The Box Problem
- 7.3.4 The Can Problem
- 7.3.5 The Wire-Cutting Problem
- 7.4 Related Rates
- 7.4.1 The Pebble Problem
- 7.4.2 The Ladder Problem
- 7.4.3 The Baseball Problem
- 7.4.4 The Blimp Problem
- 7.4.5 Math Anxiety
8. Curve Sketching
- 8.1 Introduction
- 8.1.1 An Introduction to Curve Sketching
- 8.1.2 Three Big Theorems
- 8.1.3 Morale Moment
- 8.2 Critical Points
- 8.2.1 Critical Points
- 8.2.2 Maximum and Minimum
- 8.2.3 Regions Where a Function Increases or Decreases
- 8.2.4 The First Derivative Test
- 8.2.5 Math Magic
- 8.3 Concavity
- 8.3.1 Concavity and Inflection Points
- 8.3.2 Using the Second Derivative to Examine Concavity
- 8.3.3 The Möbius Band
- 8.4 Graphing Using the Derivative
- 8.4.1 Graphs of Polynomial Functions
- 8.4.2 Cusp Points and the Derivative
- 8.4.3 Domain-Restricted Functions and the Derivative
- 8.4.4 The Second Derivative Test
- 8.5 Asymptotes
- 8.5.1 Vertical Asymptotes
- 8.5.2 Horizontal Asymptotes and Infinite Limits
- 8.5.3 Graphing Functions with Asymptotes
- 8.5.4 Functions with Asymptotes and Holes
- 8.5.5 Functions with Asymptotes and Critical Points
9. The Basics of Integration
- 9.1 Antiderivatives
- 9.1.1 Antidifferentiation
- 9.1.2 Antiderivatives of Powers of x
- 9.1.3 Antiderivatives of Trigonometric and Exponential Functions
- 9.2 Integration by Substitution
- 9.2.1 Undoing the Chain Rule
- 9.2.2 Integrating Polynomials by Substitution
- 9.3 Illustrating Integration by Substitution
- 9.3.1 Integrating Composite Trigonometric Functions by Substitution
- 9.3.2 Integrating Composite Exponential and Rational Functions by Substitution
- 9.3.3 More Integrating Trigonometric Functions by Substitution
- 9.3.4 Choosing Effective Function Decompositions
- 9.4 The Fundamental Theorem of Calculus
- 9.4.1 Approximating Areas of Plane Regions
- 9.4.2 Areas, Riemann Sums, and Definite Integrals
- 9.4.3 The Fundamental Theorem of Calculus, Part I
- 9.4.4 The Fundamental Theorem of Calculus, Part II
- 9.4.5 Illustrating the Fundamental Theorem of Calculus
- 9.4.6 Evaluating Definite Integrals
- 9.5 Trigonometric Substitution Strategy
- 9.5.1 An Overview of Trigonometric Substitution Strategy
- 9.5.2 Trigonometric Substitution Involving a Definite Integral: Part One
- 9.5.3 Trigonometric Substitution Involving a Definite Integral: Part Two
- 9.6 Numerical Integration
- 9.6.1 Deriving the Trapezoidal Rule
- 9.6.2 An Example of the Trapezoidal Rule
10. Applications of Integration
- 10.1 Motion
- 10.1.1 Antiderivatives and Motion
- 10.1.2 Gravity and Vertical Motion
- 10.1.3 Solving Vertical Motion Problems
- 10.2 Finding the Area between Two Curves
- 10.2.1 The Area between Two Curves
- 10.2.2 Limits of Integration and Area
- 10.2.3 Common Mistakes to Avoid When Finding Areas
- 10.2.4 Regions Bound by Several Curves
- 10.3 Integrating with Respect to y
- 10.3.1 Finding Areas by Integrating with Respect to y: Part One
- 10.3.2 Finding Areas by Integrating with Respect to y: Part Two
- 10.3.3 Area, Integration by Substitution, and Trigonometry
- 10.4 The Average Value of a Function
- 10.4.1 Finding the Average Value of a Function
- 10.5 Finding Volumes Using Cross-Sections
- 10.5.1 Finding Volumes Using Cross-Sectional Slices
- 10.5.2 An Example of Finding Cross-Sectional Volumes
- 10.6 Disks and Washers
- 10.6.1 Solids of Revolution
- 10.6.2 The Disk Method along the y-Axis
- 10.6.3 A Transcendental Example of the Disk Method
- 10.6.4 The Washer Method across the x-Axis
- 10.6.5 The Washer Method across the y-Axis
- 10.7 Shells
- 10.7.1 Introducing the Shell Method
- 10.7.2 Why Shells Can Be Better Than Washers
- 10.7.3 The Shell Method: Integrating with Respect to y
- 10.8 Work
- 10.8.1 An Introduction to Work
- 10.8.2 Calculating Work
- 10.8.3 Hooke's Law
- 10.9 Moments and Centers of Mass
- 10.9.1 Center of Mass
- 10.9.2 The Center of Mass of a Thin Plate
- 10.10 Arc Lengths and Functions
- 10.10.1 An Introduction to Arc Length
- 10.10.2 Finding Arc Lengths of Curves Given by Functions
11. Differential Equations
- 11.1 Separable Differential Equations
- 11.1.1 An Introduction to Differential Equations
- 11.1.2 Solving Separable Differential Equations
- 11.1.3 Finding a Particular Solution
- 11.1.4 Direction Fields
- 11.1.5 Euler's Method for Solving Differential Equations Numerically
- 11.2 Growth and Decay Problems
- 11.2.1 Exponential Growth
- 11.2.2 Logistic Growth
- 11.2.3 Radioactive Decay
12. L'Hôpital's Rule and Improper Integrals
- 12.1 Indeterminate Quotients
- 12.1.1 Indeterminate Forms
- 12.1.2 An Introduction to L'Hôpital's Rule
- 12.1.3 Basic Uses of L'Hôpital's Rule
- 12.1.4 More Exotic Examples of Indeterminate Forms
- 12.2 Other Indeterminate Forms
- 12.2.1 L'Hôpital's Rule and Indeterminate Products
- 12.2.2 L'Hôpital's Rule and Indeterminate Differences
- 12.2.3 L'Hôpital's Rule and One to the Infinite Power
- 12.2.4 Another Example of One to the Infinite Power
- 12.3 Improper Integrals
- 12.3.1 The First Type of Improper Integral
- 12.3.2 The Second Type of Improper Integral
- 12.3.3 Infinite Limits of Integration, Convergence, and Divergence
13. Math Fun
- 13.1 Paradoxes
- 13.1.1 An Introduction to Paradoxes
- 13.1.2 Paradoxes and Air Safety
- 13.1.3 Newcomb's Paradox
- 13.1.4 Zeno's Paradox
- 13.2 Sequences
- 13.2.1 Fibonacci Numbers
- 13.2.2 The Golden Ratio
- 13.3 The Close of Calculus AB
- 13.3.1 A Glimpse Into Calculus II
About the Author
Edward Burger
Williams College
Edward Burger, Professor of Mathematics at Williams College, earned his Ph.D. at the University of Texas at Austin, having graduated summa cum laude with distinction in mathematics from Connecticut College.
He has also taught at UT-Austin and the University of Colorado at Boulder, and he served as a fellow at the University of Waterloo in Canada and at Macquarie University in Australia. Prof. Burger has won many awards, including the 2001 Haimo Award for Distinguished Teaching of Mathematics, the 2004 Chauvenet Prize, and the 2006 Lester R. Ford Award, all from the Mathematical Association of America. In 2006, Reader's Digest listed him in the "100 Best of America". After completing his tenure as Gaudino Scholar at Williams, he was named Lissack Professor for Social Responsibility and Personal Ethics.
Prof. Burger is the author of over 50 articles, videos, and books, including the trade book, Coincidences, Chaos, and All That Math Jazz: Making Light of Weighty Ideas and of the textbook The Heart of Mathematics: An Invitation to Effective Thinking. He also speaks frequently to professional and public audiences, referees professional journals, and publishes articles in leading math journals, including The Journal of Number Theory and American Mathematical Monthly. His areas of specialty include number theory, Diophantine approximation, p-adic analysis, the geometry of numbers, and the theory of continued fractions.
Prof. Burger's unique sense of humor and his teaching expertise combine to make him the ideal presenter of Thinkwell's entertaining and informative video lectures.
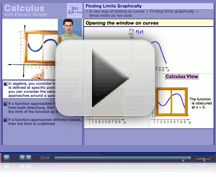
Sample Video Lessons
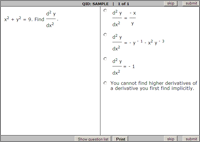
Sample Interactive Exercises
Sample Illustrated Notes
